Complex Arithmetic

“If maths is so great, why isn’t there a Maths 2?”

^{- some silly goose who didn’t anticipate complex arithmetic}

It’s the counting you know and love, but now even more imaginary than before! Instead of simple, boring, real-number land, we’re venturing into the funky terrain of manipulating complex numbers now, woohoo!

For the most part, arithmetic with complex numbers can be performed just by considering the imaginary unit $i$ to be like any other old variable, then sprinkling in a bit of algebra to push things around.

Magenta colour-coding

All imaginary parts in expressions on this page will be highlighted a lovely shade of magenta, to make them easier to follow.

_{Yes, this took way too long to typeset.}

Addition

Real

Add the real number to the real part. That’s it.

$$\begin{array}{rl}& (a+bi)+c\\ =& (a+c)+bi\end{array}$$

Complex

To add two complex numbers together, you simply add the real and imaginary parts separately. Simples!

$$\begin{array}{rl}& (a+bi)+(c+di)\\ =& (a+c)+(b+d)i\end{array}$$

Example

todo

Subtraction

Real

I’m not gonna insult your intelligence by explaining this to you.¹ Go on, click the link. You’ll figure it out. I believe in you. [[Complex Arithmetic#Addition#Real]]

Complex

Just like with the addition of complex numbers shown above, we can subtract the real and imaginary parts separately:

$$\begin{array}{rl}(a+bi)& -(c+di)\\ =(a-c)& +(b-d)i\end{array}$$

Example

todo

Multiplication

Real

Multiplying a complex number by a real number is dead simple - just multiply out the brackets! Even a toddler can do this while blindfolded and suspended upside down, so you have no excuse here.

$$\begin{array}{rl}& (a+bi)\times c\\ =& ca+cbi\end{array}$$

Complex

When multiplying two complex numbers, we take a very similar approach of multiplying everything out:

$$\begin{array}{rl}& (a+bi)(c+di)\\ =& a(c+di)+bi(c+di)\\ =& ac+adi+bci+bd{i}^2\end{array}$$

Since we know that $i^2=-1$, the last term can be simplified:

$$\begin{array}{rl}& ac+adi+bci-bd\\ =& (ac-bd)+(ad+bc)i\end{array}$$

Some people like to memorise the last step of the working above as a formula. I’m not a fan of that. Just do the middle-school algebra please.

Example

todo

Division

A-ha! Addition, subtraction and multiplication of complex numbers has been mere child’s play; division is our first taste of things starting to get slightly spicy~

Real

Just like with addition and subtraction, dividing a complex number by a real number isn’t too different from multiplication - we can still just distribute the operation across the real and imaginary parts. After all, division is the same as multiplying by the reciprocal:

$$\begin{array}{rl}& \frac{a+bi}{c}\\ =& \frac{1}{c}(a+bi)\\ =& \frac{a}{c}+\frac{b}{c}i\end{array}$$

Warning

make sure $c\ne 0$ or Bad Things™️ will happen!

Complex

Let’s try to do the same thing as if we were [[#Division#Real|dividing by a real number]]:

$$\begin{array}{rl}& \frac{a+bi}{c+di}\\ =& \frac{a}{c+di}+\frac{bi}{c+di}\end{array}$$

…aaaaand we’re stuck. This is no good; we can’t simplify this into $a+bi$ form!

Instead, let’s introduce a new tool from our mathematical toolbox: the complex conjugate. This tool is powerful, because when multiplied, it can turn any complex number into a real number. As such, we can use it to make the denominator real!

$$\begin{array}{rl}& \frac{a+bi}{c+di}\\ =& \frac{a+bi}{c+di}\times \frac{c-di}{c-di}\\ =& \frac{(a+bi)(c-di)}{c^2+d^2}\end{array}$$

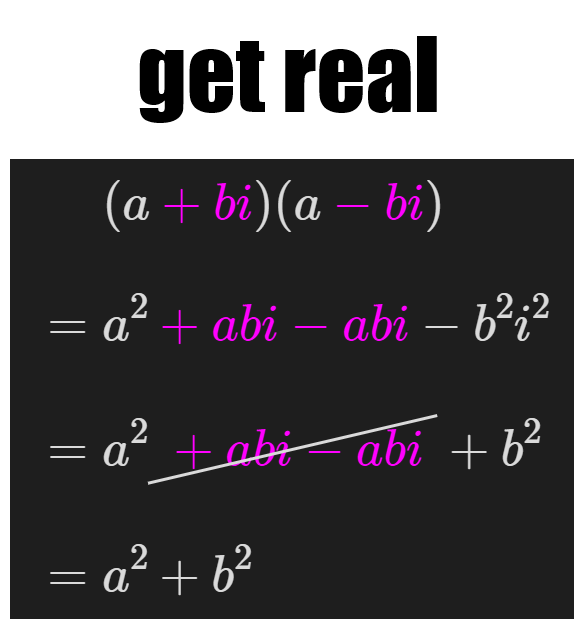
From here, we can [[#Multiplication#Complex|multiply out the numerator]]:

$$=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2}$$

Then finally, we can [[#Division#Real|divide the complex numerator by the real denominator]] to get our nice and pretty $a+bi$ form:

$$=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i$$

“Nice and pretty”…

The algebra looks horrible, but it’s cleaner with actual numbers; I promise. Again, you’d be a couple backslashes short of a LaTeX expression to memorise the above result as a formula instead of just using the intuitive method demonstrated above.

Example

todo

Footnotes

1. That was a lie; I’d absolutely insult your intelligence. Many times over. Adding a sprinkle of snarkiness to these notes gives it a unique flair and makes them more fun to write, you see. ↩